Begin with a line BD of any length.

Or, an ellipse of any shape.  (See: further below)

Extend line BD by one-half with line EB.



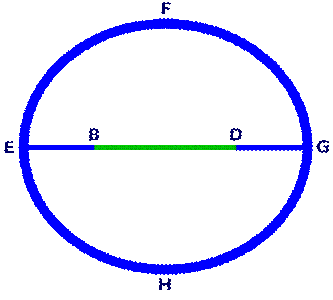
Construct an ellipse EFGH
with points B and D as the foci and
line EB as the perigee.
Thus, line ED is the apogee.

Draw line DG which will equal line EB.



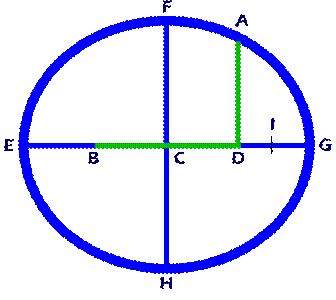
At the midpoint, C, of line BD,
draw line FH perpendicular to line BD.

Line FH intersects ellipse EFGH at points F and H.

At focus D,
draw line AD perpendicular to line BD.
Line AD intersects ellipse EFGH at point A.

Bisect line DG at Point I.

Line DI equals line GI.
 

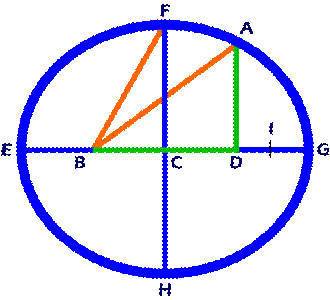
Draw Line AB.

Draw Line BF.

The definition of an ellipse is
a plane curve comprised of a
locus of points such that
the sum of the distances from
every point on the locus to
two fixed points is equal.

Thus, line AB plus line AD equals
line BE plus line BG, which equals
two times line BF, and so on.

Points B and D are the fixed points of
ellipse EFGH, each of which is a focus.

If line DI equals one, “1,”
line DG equals two, “2.”

By the definition of an ellipse:
lines AB plus AD equal eight, “8,”
as they are twice line CG
that is twice line DG.

Triangle ABD is a right triangle;
thus, line AD equals, three “3”;
line BD equals four, “4”; and,
line AB equals, five “5.”

Line BG equals, six “6”;
line EI equals, seven “7”; and,
line EG equals, eight “8.” 

If line EG equals eight, “8,”
line BF that is drawn from
a focus to a midpoint equals four, “4.”

From a line of any  length
the Natural integer values of
the first eight integers
are established from an ellipse
that is seminal phenomenon;
such that a value of “one”
is established,
within the system of numbers,
without a predetermined “base.”

To summarize:
EFGH, “E,” is an ellipse if
line BE plus line BG equals
line DE plus line DG equals
line AB plus line AD equals
2 times line BF equals
line EG.

BE + BG = DE + DG =
AB + AD = 2 x BF = EG.

And, if line AD is perpendicular to line BD,
line AB equals the square root of the
sum of line AD squared plus line BD squared.

Substituting the above line values:

2 + 6 = 6 + 2 =
5 + 3 = 2 x 4 = 8.

And, 5 = square root (9 + 16).

Let line DI, equal one, “1; and,
line BE, “2,”the perigee, “p,” = x; then,
line BF, “4,” the vector, “v,” equals x²;
line BC, “2,” the soliton. “s,” equals x² – x;
line BD, “4,” the wave, “w,” equals 2s;
line AD, “3,” the radius, “r,” equals 2x – 1;
line AB, “5,” the hypotenuse, “h,” equals w + 1;
line BG, “6,” the apogee, “o,” equals w + x;
line EI, “7,” the glyph, “g,” equals o + 1;
line GI, “1,” the key, “k,” equals p – 1;
line oP, “1,” the hypotenuse radius, “Hr,” equals k;
line EG, “8,” the major diameter, “M,” equals o + p;

Line DI is referred to as epsilon, “e.”

The radius, “oP,” of
a circle inscribed within
a right triangle equals
the product of the sides
that are opposite the hypotenuse
divided by the sum of all the sides.

oP = (AD x BD) / (AB + AD + BD)

Or, more simply, the diameter of
a circle inscribed within
a right triangle equals
the sum of the two sides
that are opposite the hypotenuse
minus the hypotenuse.

2 x oP = AD + BD – AB

Line oP, hypotenuse radius, “Hr,”
equals: (3 x 4) / (3 + 4 + 5) = 1.

2 times Line oP, hypotenuse diameter, “Hd,”
equals: 3 + 4 – 5 = 2.

 

Thus the hypotenuse radius, “Hr,” is an integer,
as are the: perigee, “p,” soliton. “s,”
vector, “v,” apogee, “o,” radius, “r,”
wave, “w,” hypotenuse, “h,”
glyph, “g,” key, “k,”
and major diameter, “M.”

 

Line FC, is the amplitude, “a.”

When the ellipse is a Brunardot Ellipse (BE)*,
and the amplitude is an integer; then,
ellipse EFGH is a Pulsoidal Ellipse (PE).
* See: below for a definition.

The following are some Pulsoidal Ellipse
integer values if perigee, “p,” equals 5;
the vector, “v,” equals p² = 25;
the soliton, “s,” equals p² – p = 20;
the wave, “w,” equals 2s = 40;
the hypotenuse, “h,” equals w + e = 41;
the radius, “r,” equals 2p – e = 9;
the amplitude, “a,” equals
p x the square root of r = 15;
the apogee, “o,” equals p + w = 45;
the glyph, “g,” equals o + e = 46;
the key, “k,” equals p – e = 4;
the hypotenuse radius, “Hr,” equals k = 4;
the major diameter, “M,” equals 2v = 50.



Draw line GH.

At focus B,
draw line BJ perpendicular to line BD;
Line BJ intersects ellipse EFGH at point J.

Draw line AJ.

Line FH is the minor diameter, “A,”
which equals 2a = 30;
Line BJ equals line AD the radius, “r”;
Line AC or CJ is the diagonal radial, “d,”
which quickly converges to s + 2 = 22;
Line AJ is the diagonal, “D,”
which quickly converges to  2d = 44.

Line GH is the diameter chord, “c.”



If the ellipse is a Brunardot Ellipse,
line oP, the hypotenuse radius, “Hr,”
equals an integer, k = 4.

If the ellipse is a Pulsoidal Ellipse,
interger values for the other
inscribed circles are:

Line oV, the vector radius, “Vr,”
equals an integer, (a – p) / 2 = 5.

2 times line oR, the radial diameter, “Rd,”
converges to an integer, 2k – e = 7.

2 times line oT, the chord diameter, “Cd,”
converges to an integer, 2Vr + e = 11.
 

The Elliptical Constant,
epsilon, “e,” equals One, “1,”
has, for any ellipse, many forms;
a few equations are:

e = h – w;  e = 2p – r;
e = 2h – r²;  e = p – Hr.

For any ellipse,
when any of the above differences
equal one, or are set to one, which is the
Elliptical Constant, epsilon, “e,” equals One, “1,”
then, all the relationships, or equations that
relate the different parts of any ellipse,
are always the same set of equations that are
referred to as the Natural set of equations.

As the perigee value increases
beyond a single digit
the following equation
quickly converges to
the Elliptical Constant,
epsilon, “e,” equals One, “1”:

e = (d – s)/2;

It can be seen that the difference between
the diagonal, “d,” and the soliton, “s,”
quickly converges to
twice the Elliptical Constant.

Thus, as the perigee increases to
a value beyond small integers,
the right triangle ACD has all sides as
integers with the difference
between the base and hypotenuse
equal to two, “2”; or,
equal to twice the Elliptical Constant.

Right triangle ACD is comparable to
right triangle ABD as it has all
integer sides; however, the difference
between the base and hypotenuse
equals the Elliptical Constant.

Also, as the perigee value increases
beyond a single digit for any ellipse
the following equations:

e = Hd – Rd; and, e = Cd – Vd;

quickly converge to
the Elliptical Constant,
epsilon, “e,” equals One, “1”:

Virtually, the difference, epsilon, “e,”
between the hypotenuse diameter, “Hd,”
and the Radial diameter, “Rd,”
is minuscule;
the same is true for the difference, epsilon, “e,”
between the chord diameter, “Cd,”
and the Vector diameter, “Rd.”

These convergence differences are
on the order of
much less than10^-12
for even the smallest perigees.


Ultron Ellipses (UE), are Pulsoidal Ellipses with
the chord, ”c” as an integer.

Lemma Ellipses (LE) are Ultron Ellipses with
the lemma, “l,” as an integer.

These and other complex ellipses
are associated with elliptical bonding,
which is, heuristically, analogous to
subatomic and chemical bonding.



Line FK equals Line AB.

 Line BK, is referred to as the lemma, “l,”
which is an integer; thus, 2 times radius oL,
the lemma diameter, “Ld,” is an integer.

The Elliptical Constant can also
be constructed from  any ellipse.

Or, a line of any  length.  (See: beginning).



Begin with any ellipse, EFGH.


Bisect line EG, the major diameter, “M,”
with a perpendicular line FH,
the minor diameter, “m.”



Draw line BF equals line CE or CG
from point F to point B in line EG.



Line DG equals line EB.

From point D draw line AD,
perpendicular to line EG,
to ellipse EFGH at point A.

Draw line AB.



The Elliptical Constant, line DI,
equals line AB minus line BD.

Line IG equals line DG minus line DI.



Draw line HG.

From point B draw line BJ,
perpendicular to line EG,
to ellipse EFGH at point J.

Draw line AJ.
 
Inscribe four circles in right triangles
ABD, BCF, BCJ, and CGH.

If line DI, epsilon, “e,” = 1; and,
lines BE and DG, the perigee, “p,” = x = 13;
lines BC and CD, the soliton, “s,” p² – p = 156;
line BD, the wave, “w,” = 2s = 312;
lines BG and DE, the apogee, “o,” = w + p = 325;
line EI, the glyph, “g,” = o + e = 326;
line GI, the key, “k,” = p – e = 12
lines AD and BJ, the radius, “r,” = 2p – e = 25
lines CF and CH, the amplitude, “a,”
= p x square root of r = 65;
line BF, the vector, “v,” = p² = 169;
line AB, the hypotenuse, “h,” = w + e = 313;
lines AC and CJ, the diagonal radial, “d,”
quickly converge to s + 2e = 158;
line GH, the diameter chord, “c,”
 quickly converges to s + r = 181;
line AJ, the diagonal, “D,” = 2d,
which quickly converges to 316;
line EG, the major diameter, “M,” = 2v = 338;
line FH, the minor diameter, “A,” = 2a = 130.

Inscribed circle ABD is the hypotenuse circle.
Inscribed circle BCF is the vector circle.
Inscribed circle BCJ is the radial circle.
Inscribed circle CGH is the chord circle.

Line oP, hypotenuse radius, “Hr,” = k = 12;
line oV, the vector radius, “Vr,” = (a – p)/2 = 26;
2 x line oR, the radial diameter, “Rd,”
 quickly converges to 2k – e = 23;
2 x line oT, the chord diameter, “Cd,”
quickly converges to 2Vr + e = 53;

If epsilon, “e,” = One;
then, for any ellipse
perigee, “p,” equals x;
soliton, “s,” equals x² – x,
which is the Natural function;
vector, “v,” equals x²;
apogee, “o,” equals s + v;
radius, “r,” equals 2p – e;
wave, “w,” equals 2s;
hypotenuse, “h,” equals w + e or (r² + e) / 2;
glyph, “g,” equals o + e;
key, “k,” equals p – e;
diagonal radial, “d,” converges quickly to s + 2e;
diagonal, “D,” converges quickly to 2d
amplitude, “a,” equals p x square root of r;
minor diameter, “A,” equals 2a;
major diameter, “M,” equals 2v;
diameter chord, “c,” converges quickly to s + r;
hypotenuse radius, “Hr,” equals k;
vector radius, “Vr,” equals (a – p) / 2;
radial diameter, “Rd,” converges quickly to 2k – e;
chord diameter, “Cd,” converges quickly to 2Vr + e.

If the perigee, “p,” equals “e”;
the ellipse is a circle; and,
p, s, v, o are the first terms of
the revised  Fibonacci sequence:
1, 0, 1, 1, ...

If the soliton, “s,” equals “e”; then,
the perigee, “p,” equals the Golden Ratio, “F.”

The Brunardot Theorem (BT)
states that for any ellipse:
the square of the diameter chord, “c,”
equals two times the square of the vector, “v,”
minus the square of the soliton, “s.”


c² = 2v² – s²

A Conceptual Ellipse (CE)
is any ellipse when
epsilon, “e,” equals One.

A Brunardot Ellipse (BE) is
a Conceptual Ellipse (CE) with a
perigee, “p,” equal to any Natural integer.

A Pulsoidal Ellipse (PE) is
a Brunardot Ellipse (BE) with an
amplitude, “a,” equal to a Natural integer.

An Ultron Ellipse (UE) is
an Pulsoidal Ellipse (PE) with a
diameter chord, “c,” equal to a Natural integer.

Conceptual Ellipses (CE) can be generated by
any two positive numbers
that are referred to as
Time, “T,” and Cycle, “C.”

  Circles and straight lines
are special ellipses where
the Time, “T,” and/or Cycle, “C,”
have infinite or infinitesimal values.

Brunardot Ellipses (BE) can be generated by
any two Natural integers for the
Time, “T,” and Cycle, “C.”

Pulsoidal Ellipses (PE) can be generated by
any Brunardot Ellipse.

Ultron Ellipses (UE), Lemma Ellipses (LE),
and other complex ellipses are
generated by predictable factors
that comprise the values for the
Time, “T,” and Cycle, “C.”

 

Formulas that apply to all ellipses and
circles inscribed in right triangles
that can be used to check values are:

The Brunardot Theorem

C² = 2v² – s².

The Pythagorean Theorem

a² + b² = c².

The Inverse Square Law

v = p².

Circles inscribed in right triangles

radius = (a x b) / (a + b + c)
diameter = a + b – c.

Radial lines from a focus to
the circumference

2v = M
h + r = M
p + o = M.

A Fibonacci-like additive sequence

p,
s,
p + s = v,
s + v = o.

Of additional interest:

The Elliptical Constant,
epsilon, “e,” = One, “1,”
easily, makes possible
the construction of
the square root or
the square of any line.

Salient Natural set of Equations
derived from


The Brunardot Theorem
c² = 2v² – s²
and
The Elliptical Constant,
epsilon, “e,” = One, “1,” are:

T= Time = any Natural Integer;
C= Cycle phase = any Natural Integer.

p = TC
v = p²
s = p² – p
w = 2s
h = w + e
r = 2p – e
k = p – e.

And, for Pulsoidal Ellipses:
Ellipticalness = TC;
2TC – e = Pulsoidal factor, “F,”;
r = F²;
a = Fp.

Page 25

 

                                            T

 

EllipticalConstant.com website The Elliptical Constant (EC) is the Primary, Universal, True Constant that establishes the value of . . ."ONE!" © Copyright 2005-17 by CONCEPTUAL Applications Terms:  Brunardot, and Pulsoid Theory must be cited. CONCEPTUAL Applications Family of Informational Websites  Emphasizing Philogic, a discipline that overarches Science, Theology, and Philosophy (STP) Website Design by:   CONCEPTUAL  Applications a division of: WebComm21